Régression Logistique : Précision et Probabilité en ML

La régression logistique est une méthode statistique largement utilisée dans le domaine de l'apprentissage automatique (machine learning) pour résoudre des problèmes de classification. Bien que son nom contienne le terme "régression", elle est utilisée pour des tâches de classification binaire, où l'objectif est de prédire une variable de sortie qui est de nature catégorielle. Voici un aperçu de la façon dont fonctionne la régression logistique dans le machine learning. Elle est basée sur la fonction logistique, également connue sous le nom de fonction sigmoïde. Cette fonction a une courbe en forme de S et peut prendre n'importe quel nombre réel en entrée, mais sa sortie est toujours comprise entre 0 et 1. Cela la rend idéale pour estimer des probabilités.

Dans le contexte du machine learning, la régression logistique estime la probabilité qu'une observation donnée appartienne à une classe particulière. Par exemple, dans un contexte médical, elle pourrait être utilisée pour prédire la probabilité qu'un patient ait une certaine maladie, en se basant sur des caractéristiques telles que l'âge, le poids et le cholestérol.

Processus de Modélisation

• Modèle Mathématique :
• Le modèle de régression logistique utilise une équation linéaire de la forme     z = w1x1 + w2x2 + ... + wnxn + b   , où     w   représente les poids (coefficients),     x   les caractéristiques (features) et     b   le terme de biais.
• La valeur     z   est ensuite transformée à l'aide de la fonction sigmoïde pour obtenir une probabilité :     p = 1 / (1 + e^-z)   .
• Estimation des Probabilités :
• Cette probabilité     p   représente la probabilité que l'observation appartienne à la classe 1 (par exemple, "malade"). La probabilité d'appartenir à la classe 0 (par exemple, "non malade") est alors     1 - p   .
• Seuil de Décision :
• Un seuil est fixé (souvent 0,5) pour décider de la classe d'appartenance. Si     p   est supérieur au seuil, l'observation est classée dans la classe 1, sinon dans la classe 0.

Entraînement du Modèle

Le processus d'entraînement d'un modèle de régression logistique implique de trouver les valeurs des poids    w    et du terme de biais    b     qui minimisent une fonction de coût, généralement la fonction de coût logistique (aussi appelée log loss). Ceci pour plusieurs raisons:

• Modélisation Précise de la Relation entre Variables :
• Les poids w et le biais b dans la régression logistique déterminent comment chaque variable indépendante influence la probabilité prédite. Ajuster ces paramètres permet au modèle d'aligner au mieux ses prédictions avec les données réelles.
• Minimisation de l'Erreur de Prédiction :
• La fonction de coût logistique mesure l'erreur entre les probabilités prédites par le modèle de régression logistique et les valeurs réelles (0 ou 1 dans le cas de la classification binaire). Minimiser cette fonction de coût signifie réduire l'erreur de prédiction du modèle, rendant ainsi ses prédictions aussi précises que possible. Voici comment elle fonctionne :
• Dans un cadre de classification binaire, la fonction de coût logistique est définie pour une seule observation comme : Log Loss=−[ylog(p)+(1−y)log(1−p)]
• Ici, y est la valeur réelle de la classe (0 ou 1) et p est la probabilité prédite par le modèle que y=1.
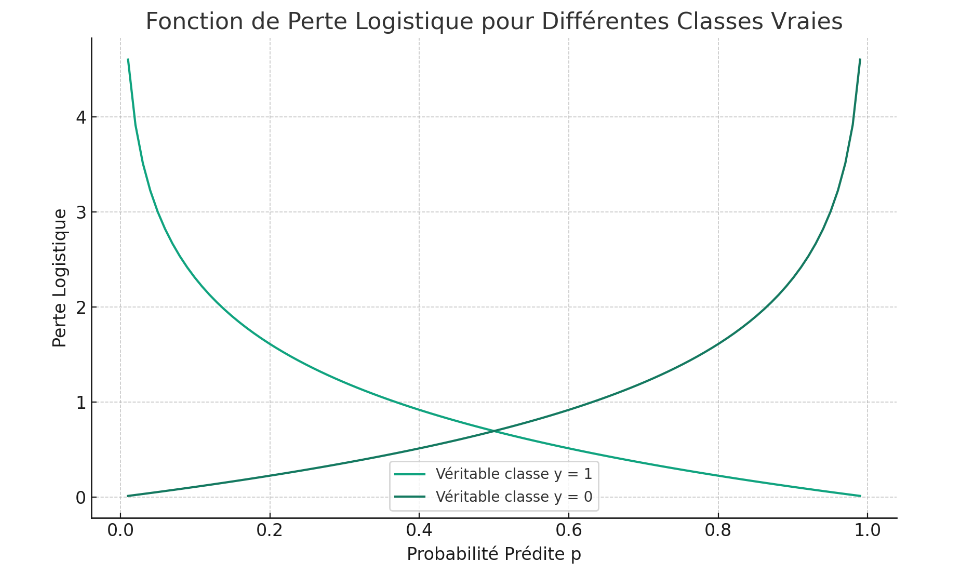
• Cette fonction pénalise les prédictions qui sont éloignées de la réalité. Si la valeur réelle y est 1 et le modèle prédit p proche de 1, la pénalité (ou le coût) est faible. Mais si le modèle prédit p loin de 1 (par exemple, proche de 0), la pénalité est élevée. De même, si y est 0 et p est prédit proche de 0, la pénalité est faible. Mais si p est prédit proche de 1, la pénalité est élevée (voir graphique "Fonction de Perte Logistique pour Différentes Classes Vraies" ci-dessous).
• Lors de l'entraînement d'un modèle de régression logistique, l'objectif est de trouver les paramètres (poids et biais) qui minimisent la fonction de coût logistique sur l'ensemble du jeu de données.
• Cela signifie que le modèle est entraîné pour faire des prédictions de probabilité aussi proches que possible des valeurs réelles des étiquettes.
• Interprétabilité des Résultats :
• En ajustant les poids pour minimiser la fonction de coût logistique, le modèle final fournit non seulement des probabilités précises mais permet également une interprétation claire de l'impact de chaque variable indépendante sur la probabilité prédite
• Utilisation d'Algorithmes d'Optimisation Efficaces :
• Les algorithmes comme la descente de gradient peuvent être utilisés efficacement pour minimiser cette fonction de coût logistique. Ces méthodes ajustent progressivement les poids de manière itérative pour atteindre le minimum de la fonction de coût. Je vous promets que nous aurons l'opportunité de voir comment cela fonctionne plus en détail dans notre blog dans un article exclusivement dédié à ce sujet.