Introduction à la Recherche Opérationnelle : Histoire et Fondements

La Recherche Opérationnelle (RO), souvent désignée par le terme Operations Research en anglais, est une discipline scientifique dédiée à l'application de méthodes analytiques avancées pour aider à prendre de meilleures décisions. Cet article vise à explorer les origines historiques et les fondements de la RO, soulignant comment cette discipline a évolué et continue d'influencer divers domaines allant de la logistique militaire à la gestion d'entreprises.

La RO trouve ses racines dans les efforts militaires de la Seconde Guerre mondiale. Face à des défis logistiques et stratégiques complexes, les Alliés ont rassemblé des scientifiques et des mathématiciens pour améliorer l'efficacité de leurs opérations. L'un des exemples les plus célèbres est celui de la Battle of Britain, où les analystes ont utilisé la RO pour optimiser l'utilisation des radars et la distribution des avions de chasse, contribuant ainsi de manière significative à la défense du Royaume-Uni.

Après la guerre, les principes et techniques de la RO ont rapidement été adoptés par le secteur public et privé. Des domaines comme la logistique, la production industrielle, les télécommunications et plus tard, la finance, ont bénéficié des méthodes analytiques développées pendant la guerre. Des institutions académiques ont commencé à offrir des cours et des programmes dédiés, formalisant ainsi la discipline.

Au cœur de la RO se trouvent plusieurs domaines clés :

• Programmation Linéaire : C'est l'une des techniques fondamentales en RO. Elle consiste à optimiser (maximiser ou minimiser) une fonction linéaire, sous des contraintes également linéaires. Elle est utilisée pour résoudre des problèmes de planification, d'allocation de ressources, de production, et plus encore.
• Programmation en Nombres Entiers et Programmation en Nombres Entiers Mixtes : Cette méthode est similaire à la programmation linéaire, mais elle exige que certaines ou toutes les variables de décision soient des entiers. Elle est particulièrement utile dans les problèmes de planification et de programmation où les solutions fractionnaires ne sont pas pratiques ou possibles.
• Programmation Non Linéaire : Elle traite des problèmes où la fonction objectif ou les contraintes sont non linéaires. Elle est utile dans des domaines tels que la gestion de portefeuille en finance, l'optimisation de processus chimiques, ou la conception de réseaux.
• Théorie des Graphes et Réseaux : Utilisée pour modéliser et résoudre des problèmes impliquant des réseaux, comme les problèmes de chemin le plus court, de flux maximal, ou de planification de transport.
• Théorie des Files d'Attente : Cette méthode analyse les files d'attente pour aider à optimiser le service dans des domaines comme les télécommunications, les centres d'appels, et les systèmes de santé.
• Recherche Heuristique et Métaheuristique : Ces techniques incluent des algorithmes comme la recherche tabou, l'algorithme génétique, et le recuit simulé. Elles sont utilisées pour trouver des solutions approchées dans des problèmes où une recherche exhaustive est impraticable.
• Méthodes de Simulation : La simulation Monte Carlo ou la simulation basée sur des agents sont des exemples où les scénarios complexes sont modélisés pour évaluer les performances ou prévoir les résultats dans des situations incertaines.
• Optimisation Stochastique : Elle se concentre sur les problèmes d'optimisation où certains paramètres sont incertains ou aléatoires, typique dans la gestion des stocks et la planification financière.
• Analyse Multicritère : Utilisée pour prendre des décisions dans des situations où plusieurs objectifs doivent être considérés et où il n'existe pas de solution unique optimale.

Un exemple classique d'application de la programmation linéaire en recherche opérationnelle est le problème d'optimisation de la production dans une usine. Imaginons une usine qui fabrique deux types de produits, appelons-les Produit A et Produit B. L'objectif est de maximiser les profits tout en tenant compte des contraintes de production et de ressources. Voici comment on pourrait structurer ce problème :

Objectif : Maximiser le profit total.

Fonction Objectif :

Supposons que chaque unité du Produit A génère un profit de 20€ et chaque unité du Produit B génère un profit de 30€. Si x représente le nombre d'unités du Produit A à produire et y le nombre d'unités du Produit B, la fonction objectif à maximiser est :

Profit=20x+30y

Contraintes :

• Contrainte de Temps de Production : Supposons que l'usine dispose de 500 heures de travail disponibles par semaine. Produit A nécessite 1 heure de travail par unité, et Produit B nécessite 2 heures. Ainsi, la contrainte peut être exprimée comme : x+2y≤500
• Contrainte de Matière Première : Imaginons que l'usine ait 300 kg de matière première disponible par semaine. Produit A nécessite 2 kg par unité, et Produit B 3 kg. La contrainte devient : 2x+3y≤300
• Contraintes Non Négatives : Le nombre d'unités produites ne peut pas être négatif : x≥0,y≥0

Le problème peut maintenant être formulé comme suit :

Maximiser 20x+30y

Sous les contraintes :

x+2y≤500

2x+3y≤300

x≥0,y≥0

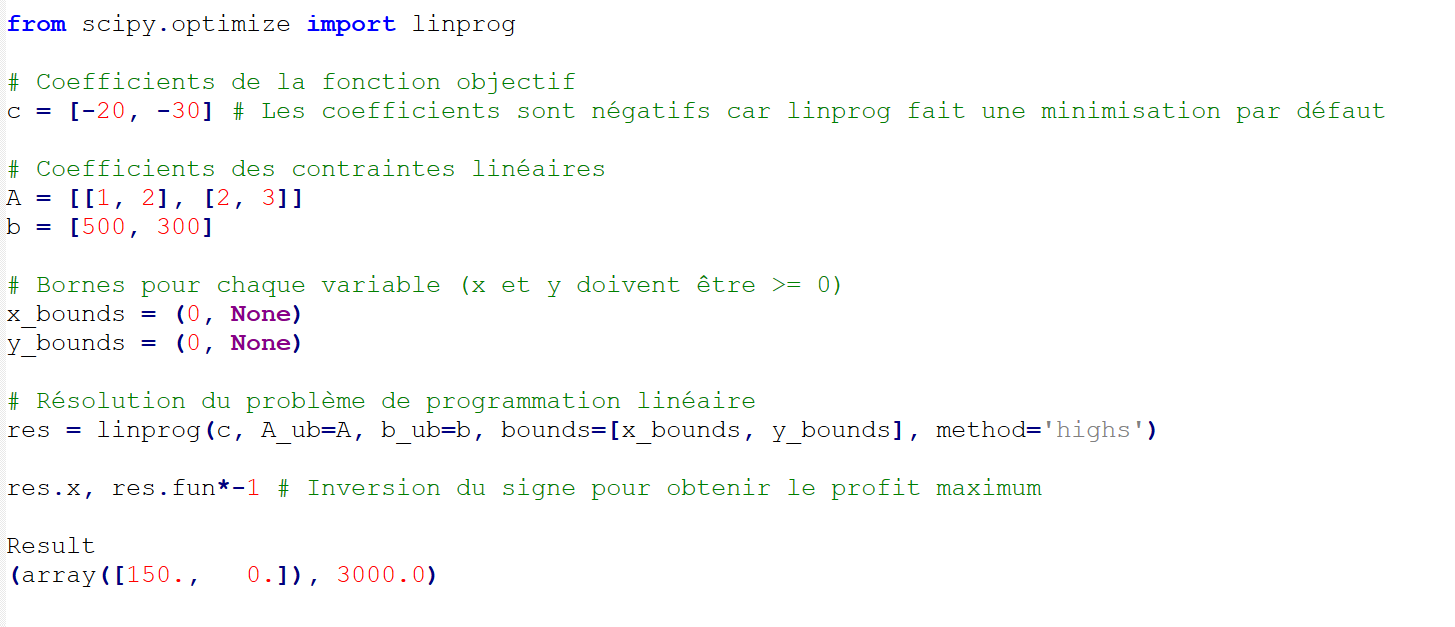
Pour résoudre ce problème, on utilise des méthodes de programmation linéaire comme la méthode du simplexe ou des logiciels spécialisés. La solution donnera le nombre optimal d'unités à produire pour chaque produit afin de maximiser le profit tout en respectant les contraintes de temps de production et de matières premières. La solution optimale du problème de programmation linéaire est de produire 150 unités du Produit A et aucune unité du Produit B. Cette stratégie de production maximisera le profit, qui sera de 3000€.